Thinking Inside the Box
Our robot has five distance sensors (VL53L0X ToF sensors): three at the front (facing ahead and +/–45 degrees), and two at both sides (facing left and right). These sensors are great for things like wall following, but can we use them for determining the robot’s position and orientation inside the arena?
The sensors can detect the walls of an empty arena quite reliably – but their usable range is slightly less than ideal: only around 128 cm. So depending on the position and orientation of the robot, there will be blind spots, where not all our sensors will “see” a wall, but most of the time, we will get some hits.
Given that we know the exact dimensions of the arena, if we have enough data points, it should be possible to determine our distance from two adjacent walls. This should give us our exact position and orientation – but only relative to one of the corners of the square: it could be any of the four. But combining this with other information (our known initial position, dead reckoning, compass reading), it should be possible to disambiguate.
So let’s say we have some measurements from some of our sensors (either from all of them, or maybe some are out of range). We know where the sensors are mounted on the robot, and their orientation, so we know the exact direction and distance of some parts of some walls. There are various possibilities, e.g. maybe we have three valid measurements (the others are out of range), but all of them can “see” the same wall. Or maybe the first two are hitting the same wall and the third one another wall. Or maybe all five sensors are in range, and we can “see” three walls. And so on…
To rephrase the problem: given three or more points (coordinates of where our distance measurements “hit” something) that fall on at least two sides of a square of known size, find the position and orientation of the square, “fitting” it onto the points.
There are various clever algorithms to fit a bounding box or a minimum area rectangle on a given set of points (OpenCV has some implementations too). But these don’t really help us: our case is more special and simpler: we already know the exact size of the box we want to fit!
Even if we have at least three measurements that seem to hit at least two different sides, usually there are multiple solutions with different orientations, so we’ll have to try some combinations, see which orientation of the square matches all of our measurements, or which one is most consistent with previous values (no sudden jumps to a different corner).
Let’s look at one of the cases more closely: we have three measurements, and we’re assuming that the first two hit the same wall, with the third hitting the adjacent wall:
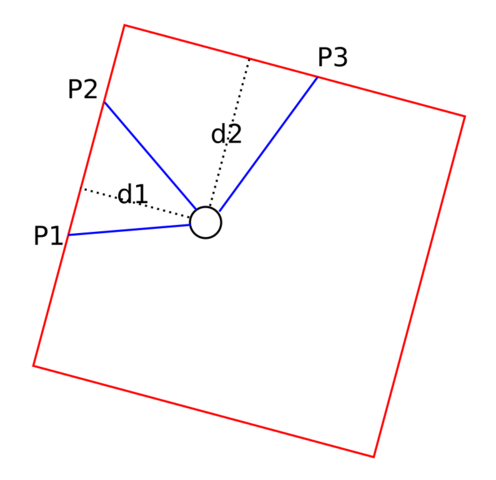
- Red box: the arena (the shape we want to detect)
- Black circle: the robot
- Blue lines: three “rays” of distance measurements, finding some edges (in reality, these would be mounted at more regular angles, we’re showing some random orientations here).
- Dotted lines (d1 and d2): distances from two edges of the arena
The first distance (d1) is easy (that is, easy to search for on StackOverflow): distance of a point (the center of the circle) from a line defined by two points (P1 and P2).
The second distance (d2) can also be determined with some trigonometry (using the fact that we know the angles of all the blue lines, and that the dotted lines for d1 and d2 are perpendicular). Once we have both distances, it’s easy to find the rotation of the square – again, we know all the angles of our blue “beams” and can also calculate the angles of the dotted lines).
Here is a solution – there is probably a more elegant way, but this seems to work:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
"""
Find the arena, assuming we're facing a corner to the left with the
first two distances hitting the same wall (left).
:param dist_points: list of coordinates of measured distances (x, y)
:param dist_vectors: measured distances as vectors (length, angle)
:returns: x, y, rot: our position and orientation in the arena
(rotated variations of this for the other corners are also valid)
"""
def arena_left_corner(dist_points, dist_vectors):
# For now, we're only using the first 3 points.
# Also, we're assuming that p1 and p2 are on one side, p3 is on the adjacent side.
[p1, p2, p3] = dist_points[:3]
(p1len, p1a) = dist_vectors[0]
(p3len, p3a) = dist_vectors[2]
# Get the distance from the line p1-p2
# https://stackoverflow.com/questions/39840030/distance-between-point-and-a-line-from-two-points
d1 = norm(np.cross(p2 - p1, p1 - np.array((0,0)))) / norm(p2 - p1)
# The angle of the line p2-p1
p1p2a = cart2angle(p2-p1)
# h1: the point where the d1 distance meets the line p1-p2
# - find the angle of the vector pointing to h1:
b = np.arccos(d1 / p1len)
h1a = p1a + b if p1a - p1p2a <= np.pi/2 else p1a - b
# Find the distance to the adjacent side:
a = h1a - np.pi/2 - p3a
d2 = np.cos(a) * p3len
# The rotation angle of the arena
rot = np.pi - h1a
return ARENA_W/2 - d1, d2 - ARENA_W/2, rot
This is of course just half of the story: we need to handle all the other possibilities, start with a known position, disambiguate between multiple corners, etc… But before all that, we can try out just the above in simulation:
- Box on the left: the simulated arena with the robot, showing the actual, “real” movement
- Red square on the left: overlaid on the real one, this shows what we detect as the arena
- Box on the right: the robot’s detected position and orientation: our ultimate goal is for this to match what’s on the left
We can see that as long as our assumptions from the above limited case are correct (we’re mostly facing the top left corner), we can detect the position and orientation quite accurately.
If we move to face another corner, the detected square on the left still seems to match the real arena, but the robot’s position and orientation on the right are rotated (we found a corner, but it’s not the top left one).
If we turn away completely from our “favourite” side and corner (for example when moving diagonally), our assumptions are completely wrong, and the detected values are way off.
There are also a few completely blind spots, where we can only get three measurements, all aligned on the same side: this is when we definitely can’t get any meaningful data (the robot turns red on the right). It’s actually quite hard to get into this “unfortunate” corner, and turning just a little bit is enough to “escape”.
So all this is really promising, but it needs a bit more work to be actually useful!
